LeetCode #88：合并两个有序数组

1970-01-01 00:00 (GMT+8) 阅读时间 0 分钟 LeetCodeLeetCode-Easy数组双指针排序

https://leetcode.cn/problems/merge-sorted-array/description/

题干

给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2，另有两个整数 m 和 n ，分别表示 nums1 和 nums2 中的元素数目。

请你合并 nums2 到 nums1 中，使合并后的数组同样按 非递减顺序 排列。

注意：最终，合并后数组不应由函数返回，而是存储在数组 nums1 中。为了应对这种情况，nums1 的初始长度为 m + n，其中前 m 个元素表示应合并的元素，后 n 个元素为 0 ，应忽略。nums2 的长度为 n 。

示例

示例 1：

输入：nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3

输出：[1,2,2,3,5,6]

解释：需要合并 [1,2,3] 和 [2,5,6] 。

合并结果是 [1,2,2,3,5,6] ，其中斜体加粗标注的为 nums1 中的元素。

示例 2：

输入：nums1 = [1], m = 1, nums2 = [], n = 0

输出：[1]

解释：需要合并 [1] 和 [] 。

合并结果是 [1] 。

示例 3：

输入：nums1 = [0], m = 0, nums2 = [1], n = 1

输出：[1]

解释：需要合并的数组是 [] 和 [1] 。

合并结果是 [1] 。

注意，因为 m = 0 ，所以 nums1 中没有元素。nums1 中仅存的 0 仅仅是为了确保合并结果可以顺利存放到 nums1 中。

复习：各种排序算法的复杂度（时间、空间）

目前我了解的排序算法主要有以下几种：

冒泡排序，最简单无脑的排序算法。
插入排序
选择排序
归并排序
快速排序
希尔排序
堆排序

几种算法的复杂度可以用如下表格表示：

排序算法	平均时间复杂度	最好时间复杂度	最坏时间复杂度	空间复杂度	稳定性
冒泡排序	$O (n^{2})$	$O (n)$	$O (n^{2})$	$O (1)$	稳定
插入排序	$O (n^{2})$	$O (n)$	$O (n^{2})$	$O (1)$	稳定
选择排序	$O (n^{2})$	$O (n^{2})$	$O (n^{2})$	$O (1)$	不稳定
归并排序	$O (n l o g n)$	$O (n l o g n)$	$O (n l o g n)$	$O (n)$	稳定
快速排序	$O (n l o g n)$	$O (n l o g n)$	$O (n^{2})$	$O (l o g n)$	不稳定
希尔排序	$O (n^{1.3})$ 或 $O (n l o g n)$ ^[1]	$O (n)$	$O (n^{2})$	$O (1)$	不稳定
堆排序	$O (n l o g n)$	$O (n l o g n)$	$O (n l o g n)$	$O (1)$	不稳定

基础解法：调用原生函数

在 JavaScript 中可以调用原生函数 concat 和 sort 来完成合并和排序。其中 concat 的底层实现是创建一个新的数组，并将两个数组的元素逐一添加到新数组中，因此时间复杂度为 O(n)。sort 稍微复杂一些，根据元素数量不同使用不用的排序算法：

当元素数量小于等于 22 时，使用插入排序，平均时间复杂度为 $O (n^{2})$ ，最坏时间复杂度为 $O (n^{2})$ ；
当元素数量大于 22 时，使用双路快排，平均时间复杂度为 $O (n l o g n)$ ，最坏时间复杂度为 $O (n^{2})$ ；
当元素数量大于 1000 时，使用三路快排，平均时间复杂度为 $O (n l o g n)$ ，最坏时间复杂度为 $O (n^{2})$ 。三路快排相比双路快排的主要优势是能更好地处理重复元素，但并不能完全避免快排算法在最坏情况（数组已经有序）下的时间复杂度为 $O (n^{2})$ 。

可以在这里看到 v8 对于 sort 的实现。

此外，如果不传入任何参数的话，v8 sort 会默认把传入的元素当做字符串来排序，因此在写题解时需要给 sort 传入比较函数。

不过这道题的 nums1 长度是最终数组全长（多余数字用 0 填充），这个可以理解，毕竟像 C 还有 Go 之类的语言来说数组长度是固定的，因此 nums1 的长度也应该固定。不过要求直接修改 nums1 但又不让返回这点我有点玩不太来，明明在自己 console 上面测了 nums1 = nums1.slice(0, m).concat(nums2).sort((a, b) => a - b) 是有效的，但是提交上去发现 nums1 并没有被修改。最后只能在第二行写了一个 forEach 来完成赋值。

因此我一开始想到的是直接把等于 0 的元素过滤掉，然后调用 sort 排序，再把 nums1 的元素替换为排序后的元素。结果没考虑到 0 是有效值的情况，排序 [-1,0,0,3,3,3,0,0,0] 就会出问题。最后使用了 slice 方式来完成有效数组的提取（因为题解已经给出了有效数字个数）。正好 slice 取头不取尾，所以也不用考虑 m，n 要不要减去 1。

TypeScript

/**
 Do not return anything, modify nums1 in-place instead.
 */
function merge(nums1: number[], m: number, nums2: number[], n: number): void {
  const temp = nums1
    .slice(0, m)
    .concat(nums2)
    .sort((a, b) => a - b);
  nums1.forEach((_, index) => (nums1[index] = temp[index]));
}

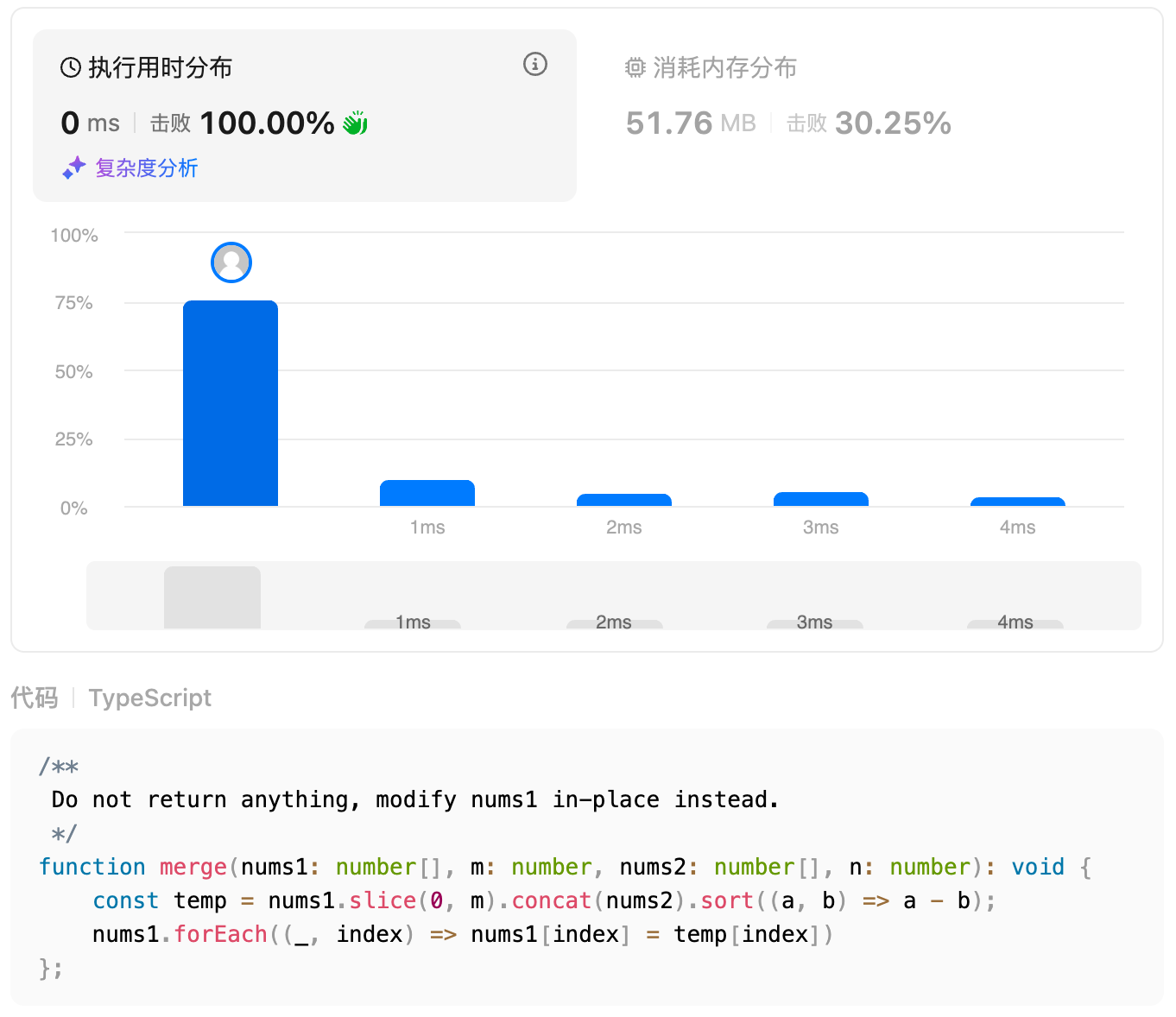
TS 版本的效率极其暴力，平均执行时间傲视群雄。就是内存……都用 JS 了，内存不溢出就算胜利了。

总结

没什么好总结的，调库就完事了。

页面历史

最后编辑于 6 个月前

查看完整历史

希尔排序的时间复杂度取决于步长序列的选择，通常认为是 $O (n^{1.3})$ 而不是 $O (n l o g n)$ ，最坏情况下为 $O (n^{2})$ 。 ↩︎

LeetCode #88：合并两个有序数组 ​

复习：各种排序算法的复杂度（时间、空间） ​

基础解法：调用原生函数 ​

总结 ​

页面历史

LeetCode #88：合并两个有序数组

复习：各种排序算法的复杂度（时间、空间）

基础解法：调用原生函数

总结