心理统计世界观：Fischer 检验、线性回归和相关、T 检验、结构方程模型（CLPM 及变体 RI-CLPM）

1970-01-01 00:00 (GMT+8) 阅读时间 0 分钟 统计结构方程模型社会科学心理

显著？不显著？

按照行业传统，在讲故事的时候我们应该先从一人一狗说起。这个人叫巴甫洛夫，狗——虽然其实不止一只——叫巴甫洛夫的狗。这个故事可能大部分人也有所耳闻：巴甫洛夫每次给狗喂食之前都会摇铃铛，久而久之，即使没有喂食，狗听到铃铛声也会开始流口水。

巴甫洛夫正在进行实验 |《野史》

鉴于巴甫洛夫在《消化腺的工作》当中似乎并没有详细描述这一实验（至少我粗翻了一遍没找到，让 Gemini 捞针也捞不出来），那么我们姑且认为这个实验设置存在一个问题：巴甫洛夫没有控制变量——也就是说，要有一组实验中的狗能听到铃铛的声音，而另一组不能。通过这种对比得到的结果才是更有信服力一些。（这个实验在 1910 年补上了）

巴甫洛夫追加的实验设置 | Wikipedia

虽然这个 bug 最后被巴甫洛夫用同一只狗自己填上了（上文链接），不过我们希望这个实验能更严谨一些，排除做实验的狗是个见到饭盆就想到小饼干就想到沙威玛就开始流口水的吃货这种可能性。因此为了验证这个实验结果是否具有一般性，财大气粗的我们决定和学校的动物中心打申请，先点上 30 条狗，不要舍不得钱。

然后我们把狗平均分成两组，每组 15 只，一组喂食前打铃，另一组喂食前不打铃，最后统计下每只狗流口水的都少（高于平时认为有流口水，低于或者等于平时就是没有），得到了下面这张表格。

	喂食前敲铃铛	喂食前不敲铃铛	列总和
敲铃时流口水	14 $(a)$	1 $(b)$	15 $(a+b)$
敲铃时不流口水	1 $(c)$	14 $(d)$	15 $(c+d)$
行总和	15 $(a+c)$	15 $(b+d)$	30 $(a+b+c+d=n)$

这张表的关系性自然是一眼盯真，但是审稿人狠狠地给了一个 revision，要求我们说明这个结果不存在偶然性，不然就要拒稿了。为了避免审稿人把我们的文章拒掉之后悄悄自己连夜让手底下的学生复制一篇自己拿去投掉，我们需要光速补上一个统计显著性证明自己的实验结果不是偶然做成这样的，换 30 条狗来做实验也能得出一样的结果。

统计学显著性无非就两种可能，显著或者不显著。为了避免陷入自我实现预言（self-fulfilling prophecy，更倾向于寻找符合假设的证据来证明自己的观点），我们比起证实假说更倾向于证伪。因此我们需要先假设实验结果不显著（归无假设 $H_0$），也就是假设狗流不流口水和打铃没有任何关系；接着我们会使用我们的实验结果来说明“假如结果是不显著的，那么我们得到的实验结果有多不寻常”——也就是统计学家常说的 $p$ 值——来证明“实验结果没有显著性”这个结果是有多么不可能，从而让我们“狗流口水和打铃有关系”的备择假设（$H_1$）成立。听起来有点绕，总之 $p$ 值越小越好。

作为 2025 年的新概念民工，我们自然要满足审稿人的要求，送他一个 Fischer 检验：

$$p=\frac{(a+b)!(c+d)!(a+c)!(b+d)!}{a!b!c!d!n!}=\frac{15!\times 15!\times 15!\times 15!}{14!\times 1!\times 1!\times 14!\times 30!}<.001$$

这么一看结果是挺小的（$p<.001$，可知“打铃和流口水实际上没有关系但是实验结果表示二者之间有关系”这一事件发生的概率小于 0.1%），但是审稿人会不会觉得我的结果不够好，要求我得满足四个 9？我的 $p$ 值等于 0.1 行不行？等于 0.15 行不行？

这就要说到统计学中的第一类错误（Type I error）和第二类错误（Type II error）了。第一类错误指的是原假设为真但是被实验结果拒绝的情况，第二类错误指的是原假设为假但是实验结果认为原假设为真的情况。我们假设第一类错误发生的概率为 $\alpha$，第二类错误发生的概率为 $\beta$，那么就能得到下面这张表格：

研究决策\真实情况	H₀ (归无假设) 为真	H₁ (备择假设) 为真
接受 $H_0$	正确决策 $(1-\alpha )$	第二类错误 $(\beta )$
拒绝 $H_0$	第一类错误 $(\alpha )$	正确决策 $(1-\beta )$

想要得出结果总要承担结果错误的风险，不过我们总希望这个风险越小越好。因此我们希望 $\alpha$ 和 $\beta$ 两者都是越小越好。然而 $\alpha$ 和 $\beta$ 也是老对头了，一个变小另一个必然变大，因此需要有一个大爹振臂一呼：都别争了，听我的，就按这个标准做！

这个大爹就是 Fischer 他老人家。他把 $\alpha$ 和 $\beta$ 的值定在了 0.05，也就是我们常说的 5% 显著性水平。在这个水平下，发生第一类错误和第二类错误的概率都是 5%，大爹觉得这是可以接受的，于是事情就这么成了。而在每个值后面都加上一个 $p<.05$ 的标注又太麻烦，于是大家就用一颗星号“*”来表示 $p<.05$，两颗星号“**”来表示 $p<.01$，三颗星号“***”来表示 $p<.001$。于是就有了论文常见的一颗星、两颗星、三颗星，以及觉得自己的数据实在不是很好看，于是用匕首符号“$†$”把 $p<.10$ 也给标注上的打工人。当然我们的结果是完全没问题的，毕竟连数据都是我临时编的嘛。(冷知识：机器学习里著名的鸢尾花数据集就是他创建的)

题外话：有部分人会建议 $n\ge 40$ 的时候改用卡方检验 (Chi-square test)，卡方检验的约束是比 Fischer 检验更宽松的（甚至是个估计值，所以 Fischer 检验还有个名字叫 Fischer's exact test），40 这个魔法数字出现的原因主要是 Fischer 检验计算量比卡方大太多了，在没有计算机的时代里一般人算不过来。现在大部分情况下社科实验这点数据还不够 CPU 热身的，直接交给计算机就完事了。

定性？定量？

Fischer 检验对于定性分析（只考虑有没有，不考虑多少）实验而言是一个非常有效的手段，然而在实际研究中我们可能希望获得更详细的结论，比如存不存在铃声响度每增加 5 分贝狗就会多流半滴口水之类的定量关系。在这种时候 Fischer 检验就无能为力了。

对 Fischer 他老人家来说更加残酷的是，实际的社会科学研究里比起非黑即白的分类（名义变量），出现更加频繁的还是排序等顺序变量（比如给四个人的重要程度排序），以及得分（比如抑郁、焦虑症状得分）之类的等距变量。并且现实当中也没有那么多机会让研究者控制变量。举一个简单的例子：假如希望研究反社会人格倾向是否和幼儿时期受到虐待有关，按照控制变量的思想，应该把所有参加实验的婴儿抓一半过来狠狠虐待，然后看两组人成年后是否存在反社会人格。新中国成立以后不准成精，想成撒旦那更不行。

总而言之，由于以上种种原因，Fischer 检验在心理学领域并没有那么好用，大部分时候只能对着数据干瞪眼。怎么办呢？这时候就要轮到我们的 old good 线性回归登场了。

相信能阅读到这篇文章的大部分读者都听说过最简单的线性方程 $y=ax+b$，这个方程描述的是两个变量 $x$ 和 $y$ 之间的线性关系，$a$ 是斜率，$b$ 是截距。但是在以“人”为研究对象的社会科学领域中，我们一般会将截距分得更细一些，变成：

$$y={\beta }_0+{\beta }_{1}x+ϵ$$

其中 ${\beta }_0$ 代表了当 $x=0$ 时 $y$ 的值，也就是没有施加任何影响因素 $x$ 时 $y$ 的初始值，代表了研究对象的初始特质，也就是真实的截距（这里画个重点，之后要用到）；而 $ϵ$ 才是真正的误差项，包括了一切没有被 $x$ 解释的变量。对于上文中提到的铃声分贝和狗的关系，假设这个结论为真，那么在结论（1）“打铃和狗流口水之间存在显著关联”的基础上，通过对实验数据进行拟合，我们还应该得到类似于下面这个回归方程的结论（2）：

$$y=6+0.2x+ϵ$$

但是且慢，这条直线是怎么来的，凭什么这个方程里 ${\beta }_1$ 的值就一定是 0.2 不能是 0.3 或者 0.1？

霍金在《时间简史》里说过“每在书里放一个公式，这本书的读者就会少一半”。而我现在已经放了三个公式了，别说读者，再放下去我自己都要看不懂了。因此在这里我只给出结论，就是空间中必然存在一条直线，使得所有数据点 $(x_i,y_i)$ 到这条直线的距离的平方和最小。求出这条直线的方法叫做最小二乘法，这个知识我们下面只会用到一次，不重要，别人问起来知道装逼就行。

那再且慢，假如空间中必然存在这条直线，那不是我随便往纸上撒一把米也能画出一条线来？那不是很没意思。

很不幸是这样的，数学就是数学，只有当实际问题为数学赋予现实意义的时候我们才能判断这条线是不是真正有意义。而好巧不巧，判断这条线是否有意义的工具——我们叫做 R 方（R-square，$R^2$）——正好也和这个距离的平方和有关。

再再且慢，既然叫做 R 方了，那它肯定不能是一个负数（有兴趣的可以自行搜索定义，两组平方和相除必然不可能出现负数）。然而相关可以是正相关（奶酪越多奶酪孔越多），也可以是负相关（奶酪孔越多奶酪越少），但是 R 方无论如何都是一个非负数，因此它可以用来（在只有一个自变量的简单线性回归里能这么玩）衡量相关性的强弱，但是如果要判断二者之间是正相关还是负相关还要多看一个 ${\beta }_1$ 的符号。我是条懒狗，有没有一个工具数值能让我看一眼就知道两个值之间的相关强度和方向性呢？

有的兄弟，有的，它就是 Pearson 相关系数 $r$。虽然它不应该这样算，不过如果你恰巧使用最小二乘法拟合出了上面的那条直线，你甚至会很惊喜地发现 $r$ 正好是 $R^2$ 的平方根。平方根自然可以是一个负数，因此相关系数 $r$ 不仅可以用来判断两个变量之间的相关性强弱，还可以用来判断相关的方向是正相关还是负相关。而要计算 $r$ 值的统计显著性 $p$ 则需要用到 t 检验，这里就暂时按下不表了。

推导过程

(1) $r=\sqrt{R^2}$ 的推导

$$\begin{array}{rcl}r=\rho (y_i,{\hat{y}}_i)& =& \frac{cov(y_i,{\hat{y}}_i)}{\sqrt{var(y_i)var({\hat{y}}_i)}}\\ & =& \frac{\sum _{i=1}^n(y_i-\overline{y})({\hat{y}}_i-\overline{y})}{\sqrt{\sum _{i=1}^n(y_i-\overline{y}{)}^2\sum _{i=1}^n({\hat{y}}_i-\overline{y}{)}^2}}\\ & =& \frac{\sum _{i=1}^n(y_i-{\hat{y}}_i+{\hat{y}}_i-\overline{y})({\hat{y}}_i-\overline{y})}{\sqrt{\sum _{i=1}^n(y_i-\overline{y}{)}^2\sum _{i=1}^n({\hat{y}}_i-\overline{y}{)}^2}}\\ & =& \frac{\sum _{i=1}^n(y_i-{\hat{y}}_i)({\hat{y}}_i-\overline{y})+\sum _{i=1}^n({\hat{y}}_i-\overline{y}{)}^2}{\sqrt{\sum _{i=1}^n(y_i-\overline{y}{)}^2\sum _{i=1}^n({\hat{y}}_i-\overline{y}{)}^2}}\\ & =& \frac{0+\sum _{i=1}^n({\hat{y}}_i-\overline{y}{)}^2}{\sqrt{\sum _{i=1}^n(y_i-\overline{y}{)}^2\sum _{i=1}^n({\hat{y}}_i-\overline{y}{)}^2}}\\ & =& \sqrt{\frac{\sum _{i=1}^n({\hat{y}}_i-\overline{y}{)}^2}{\sum _{i=1}^n(y_i-\overline{y}{)}^2}}\\ & =& \sqrt{R^2}\end{array}$$

两边同平方，得 $r^2=R^2$.而根据 $r$ 的定义，相关系数矩阵可以为负，因此 $r$ 也可以为负。

要计算 $r$ 值的信度 $p$，需要先构建 t 统计量：

$$t=\frac{\overline{x}-\mu }{\frac{\sigma }{\sqrt{n}}}$$

然后将 $\mu =0,\sigma =\sqrt{1-r^2}$ 代入公式，得到：

$$t=\frac{r}{\sqrt{1-r^2}}\sqrt{n-2}$$

然后根据自由度 $n-2$ 查表，或者使用统计软件计算 $p$ 值。至于为什么能这么算，Fischer 在 1914 年的论文里给出了证明，现在只要交给统计软件就行了。

至此，我们已经得到了一个简单线性回归方程（只有一个自变量的回归方程），并且得到了相关系数 $r$ 和信度 $p$ 值。一般情况下我们只需要汇报这两个值就可以了，但是现在诸如 Developmental Psychology 之类的心理学顶刊已经加上了“鼓励使用数学模型和预测”的标准，因此我们也可以把上面的回归方程和 $R^2$ 一起汇报上去，避免被审稿人和编辑说结果太单薄。

同一对象？不同对象？

在上面关于狗的条件反射实验中，我们采取的是对不同的对象进行单次测量得到的结果，并且通过 Fischer 检验证明了结果的显著性。不过现在我又幻想了，假如我只打铃不给狗吃的，那狗流口水的量会逐步恢复正常值吗？

现在我们可以采取两种实验设计：第一种是把全部 30 条狗全都归在一组里，只打一次铃并且收集一次数据；第二种则是沿袭上一个实验的设置，分成两组每组各 15 条狗，一组打铃给肉吃，另一组打铃但是不给肉吃，测量初始值和重复几次过后打铃时狗流口水的量。因为我们决定测量的是量而不是有无，Fischer 检验又不能用了。但是今年的 KPI 还没有完成，所以我们还是决定硬上，上 t 检验。那么用哪种实验设计呢？

t 检验：无所谓，我都会出手。

心理统计中常用的 t 检验有两种，分别是配对样本 t 检验 (paired-samples t-test) 和独立双样本 t 检验 (independent-samples t-test)。但是其实还有第三种 t 检验，叫单样本 t 检验 (one-sample t-test)。

为了捋清为什么会有 t 检验这种月下三兄贵，我们还是先从“t 检验到底在检验什么”这个问题开始解释吧。

t 检验最早是为了检验啤酒厂里用来酿酒的小麦是不是符合标准的。质检员会抽出一部分小麦，检查这些小麦的化学成分是否符合标准——自然这些被自愿抽中参加破坏性检验的小麦是不可能再放回去酿酒的，因此要检查全部的小麦并不现实，只能进行抽检。

抽样检测的本质，就是老师上课经常挂在嘴边的“用样本估计总体”。既然是估计，那么样本的均值和总体的均值必然是不一样的。差 0.1 也是差，差 10 也是差，那怎么判断样本均值和总体均值一不一样呢？（有人可能会问总体均值要怎么获得，我的理解是抽样足够多次之后样本均值就可以看作是总体均值了，参考中心极限定理）

因此用来检验两组样本均值是否存在差异的 t 检验就这么被发明出来了。

单样本 t 检验

我们先从最基础也是最原始的 t 检验——单样本 t 检验说起。

这时候有人要说了，一开始不是说 t 检验需要两组样本吗？怎么这里又变成单样本了？

因为这里的所谓“单样本”，指的是样本的来源是同一个总体（也就是单批样本），而不是指样本的容量是 1。其次，单样本检验隐含了一组样本——也就是已知均值的总体。对于单样本 t 检验来说，它检验的其实是这组样本均值和总体均值是否存在显著差异。统计学或者心理学入学考试考的最多的 t 检验也是单样本 t 检验，无他，计算量（相对）小。

虽然我已经尽力控制自己不放更多公式上来了，不过为了后面扩展到配对样本 t 检验，我需要很遗憾地在这里继续放一个单样本 t 检验的公式。假设我们有一组样本，样本容量为 $n$，样本均值为 $\overline{x}$，样本标准差为 $\sigma$，总体均值为 ${\mu }_0$。那么我们就可以通过以下公式计算出 t 统计量：

$$t=\frac{\overline{x}-{\mu }_0}{\frac{\sigma }{\sqrt{n}}}$$

t 统计量需要进行进一步计算才能得到 p 值。如果有统计软件干这种脏活累活自然最好，如果没有的话——等等，你不会在考场上偷偷看这篇文章吧——就需要根据自由度 $df=n-1$ 和 t 统计值查表了。

既然讲到了自由度，这里就顺带提一下自由度的概念。自由度（degree of freedom, df）指的是样本中可以自由变动的变量个数。在一个 t 检验中，我们能确定的是样本容量 $n$ 以及样本总和 $\sum _{i=1}^n{x}_i$。（均值和总和都可以互相计算）

因为样本总和是固定的，所以假如我们想知道其中一个样本的值（就拿第 n 个样本来举例好了），就需要将样本总和减去前 $n-1$ 个样本的值。假如样本总和是 100，那么前 n - 1 个样本的值加起来是多少并不重要，哪怕相加是 114514 都行——不过第 n 个样本的值必须是 $100-114514=-114414$。因此，样本中只有 $n-1$ 个变量是独立的，第 $n$ 个变量只能由前 $n-1$ 个变量的值计算得出，否则样本总和就变了。

因此对于单样本 t 检验来说，自由度就是样本容量减去 1。

很遗憾在我们这个实验中并没有单样本 t 检验的用武之地，因此我只能回到小麦这个例子来说明它的意义。假如一批小麦样本的某个检测均值是 0.32，而相关标准要求这个值应当高于 0.25，越高越好。对于一批确定的样本，我们肯定能算出一个均值来（废话），不过有没有可能这批样本里有一部分样本的值异常地高，把本来不合格的样本平均值硬 carry 上去了呢？

这时候我们就可以给这批样本过一个单样本 t 检验，假设算出来的 p 值是 0.006——也就是上面我们在 p 值的意义里提到的“如果我们假定这批样本是合格的，它看上去也确实合格，那么由于抽样出现误差导致它实际异常但居然检验合格的概率是 0.6%”——那么我们就可以认为这批小麦是真正的地球高质量小麦，毕竟在某个抽卡标定概率 0.6% 的游戏卡池里也没多少人能单抽第一抽就出金更别提不歪了。

配对样本 t 检验

配对样本 t 检验可以理解成单样本 t 检验的扩展。这里的“配对”的意思甚至并不是“配对样本”，而是“配对变量”。因此配对样本 t 检验还有个名字叫“相关样本 t 检验 (dependent-samples t-test)”。

这么说可能十分抽象，我们可以用一个更贴近实际的例子来说明。

假设某个药厂研制出了一种新的降糖药并且在糖尿病小鼠模型上证明有效，但是众所周知社会上的鼠鼠和温室里养出来的鼠鼠亦有差别，因此我们还需要招募一批糖尿病患者做临床试验。

实验流程是这样的：对于同一名受试者，我们会测量他服药前和服药一段时间后的血糖值，然后检查服药后的血糖值是不是真的降低了。但是降不降低这个判断可以是主观的，因此我们需要一种客观的统计手段来帮助我们断言“如果我们说这种降糖药是有效果的，我们判断正确的可能性有多大”。

那么配对样本 t 检验的“配对”一词究竟配的是什么对呢，明明从始至终我们都在同一个患者身上采血啊？

其实“配对”一词配的是“变量对”，而不是“样本对”。在这个实验中，我们测量了同一个受试者的两个变量：服药前和服药后的血糖值。而对于这两个变量来说，它们的数据来源都是同一个受试者，因此它们二者是匹配的。

同样的，在配对样本 t 检验中，我们也应当通过前 $n-1$ 个样本的值计算出第 $n$ 个样本的值。因此配对样本 t 检验的自由度也是 $n-1$。

配对样本 t 检验的公式和单样本 t 检验的思路十分相似，本质上是对差值进行的一次单样本 t 检验。我们可以从单样本 t 检验的公式一步步推导得出配对样本 t 检验的公式。

首先需要理解一件事：在配对样本 t 检验当中，我们关心的不是“给药前和给药后的状态（血糖） $X_i$ ”本身，而是“给药这个行为带来的状态（血糖）$Y_i$ 的变化”。因此我们可以合成出一个新的样本 $D$，而这个新样本就是每个受试者在给药前后的状态差值（血糖差值） $X_i-Y_i$，样本量依然为 $n$。

做到这一步，最初“比较两个相关样本”的复杂问题就被成功转换为了一个更简单的问题：这个差值样本 $D$ 的平均值 $\overline{D}$，是否显著地不为 $0$？

你看，推导到这一步，我们就已经成功地将配对样本 t 检验的场景转化为了我们熟悉的（至少假装一下熟悉吧）单样本 t 检验的场景。因为我们要检验总体均值是否不为 0，所以按照假说检验的思路，我们应当检验 $H_0:{\mu }_D=0$ 和 $H_1:{\mu }_D\ne 0$。

回看一眼单样本 t 检验的公式 $t=\frac{\overline{x}-{\mu }_0}{\frac{\sigma }{\sqrt{n}}}$，在这里我们将差值的均值 $\overline{d}$ 代入 $\overline{x}$，将总体均值 $0$ 代入 ${\mu }_0$，将样本标准差 $s_d$ 代入到 $\sigma$ 中，就得到了配对样本 t 检验的公式：

$$t=\frac{\overline{d}-0}{\frac{s_d}{\sqrt{n}}}=\frac{\overline{d}}{s_d/\sqrt{n}}$$

又因为我们之前已经说明过在配对样本 t 检验中的自由度也为 $n-1$，所以在配对样本 t 检验中的标准差 $s_d$ 就可以这样计算：

$$s_d=\sqrt{\frac{\sum _{i=1}^n(d_i-\overline{d}{)}^2}{n-1}}$$

展开整个公式，得到配对样本 t 检验的最终公式：

$$t=\frac{\overline{d}-0}{\frac{\sqrt{\frac{\sum \ast {i=1}^n(d_i-\overline{d}{)}^2}{n-1}}}{\sqrt{n}}}=\frac{\overline{d}}{\sqrt{\frac{\sum \ast {i=1}^n(d_i-\overline{d}{)}^2}{n(n-1)}}}$$

可喜可贺可喜可贺，现在我们可以进入下一个话题了：假设我们的药物确实有效，价格、宣传、地推等控制变量也和市面上的竞品降糖药一模一样，并且患者很难得地竟然都是绝对理性人，我们应该通过什么方式说服患者（或者医生）认同我们的药物疗效要比竞品更好，从而选择我们的药物呢？

独立双样本 t 检验

我们继续上一个糖尿病治疗药物的例子。假设在经过一段时间的临床试验后，我们确认这种药物是有效的，可以开始进入市场前的最后准备了。宣传部门挠秃了头，希望我们能告诉营销人员这种药物和市面上销量最好的降糖药相比效果如何。

（待续）

单因素？多因素？

一个可观测的表象背后可能有不止一个变量在推波助澜。虽然放公式是影响阅读量的原因之一，不过一篇文章（比如这篇）的阅读量惨淡自然也不完全是因为我上面放了五个公式的缘故，八成还有我选题太偏、文笔太烂、内容太水、没人认识我，或者今天我出门时迈的左脚之类的原因，这些因素共同作用导致了这篇文章阅读量惨淡。

在研究中，我们自然是希望把这些自变量（$x_1,x_2,\cdots ,x_n$）对因变量（$y$）的影响都考虑进去，得到一个更加全面的模型。我们上面用到的线性回归模型能不能做到这点呢？

能的兄弟，能的，你说的这个叫做多元线性回归模型。

（待续）

互相独立？互相影响？

Within-person? Between-person?

一张基本结构完整的 CLPM 示意图 | longitudinalanalysis.com

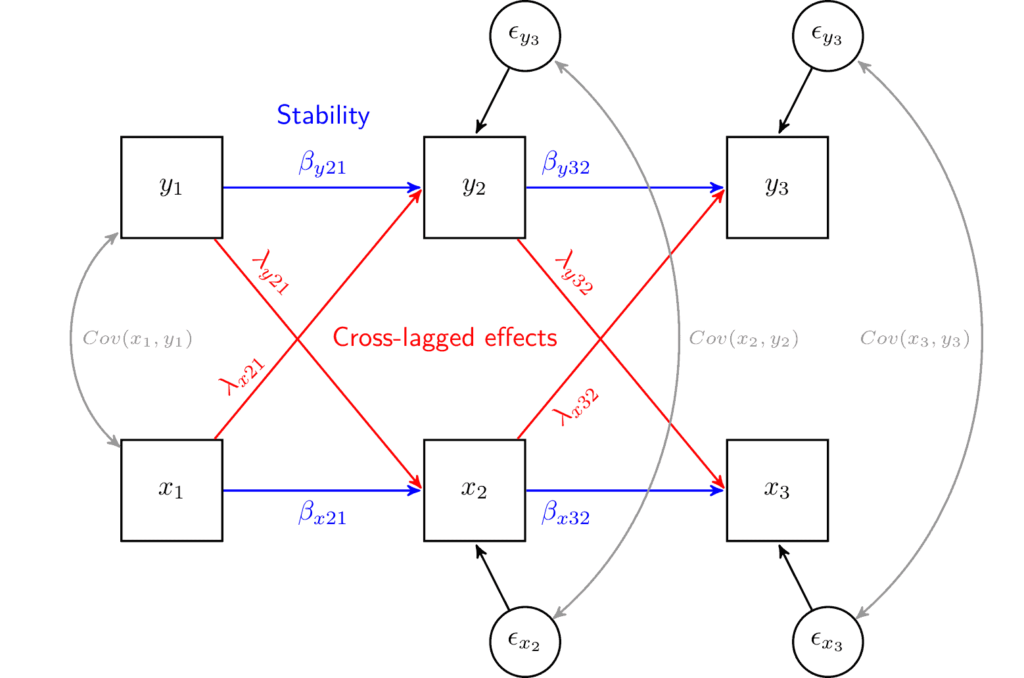
（待续）

参考和扩展阅读

• 邱嘉平著《因果推断实用计量方法》，会涵盖到这篇里没有细说的因果关系和推断
• 最小二乘法的几何原理是什么？，硬核催眠
• Confirmatory Factor Analysis in R with lavaan - UCLA OARC，我的 CFA 启蒙
• A critique of the cross-lagged panel model，RI-CLPM 开山之作
• A critique of the random intercept cross-lagged panel model，正方观点要看，反方观点也要看，这样才称得上健全

页面历史

最后编辑于 1 分钟前

查看完整历史

43b8590-docs: 填一部分统计的坑

0b5e794-docs: 心理统计世界观